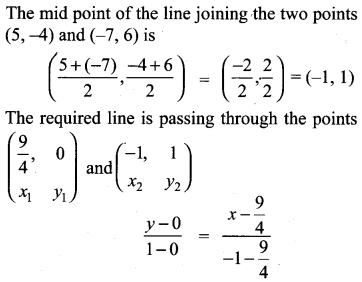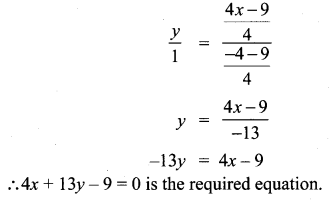Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.4
10th Maths Exercise 5.4 Samacheer Kalvi Question 1.
Find the slope of the following straight lines
(i) 5y – 3 = 0
(ii)
Solution:
Exercise 5.4 Class 10 Samacheer Kalvi Question 2.
Find the slope of the line which is
(i) parallel to y = 0.7x -11
(ii) perpendicular to the line x = -11
Solution:
(i) y = 0.7x – 11
line parallel to y = 0.7x – 11 is y = 0.7x + C
If the lines are parallel, slopes are equal
∴ The slope of the required line is 0.7.
(ii) m = tan θ = tan 90°= ∞ undefined.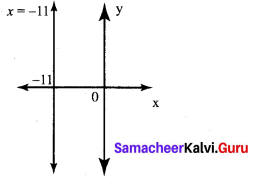
Ex 5.4 Class 10 Samacheer Question 3.
Check whether the given lines are parallel or perpendicular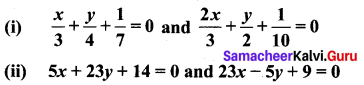
Solution:
(i) 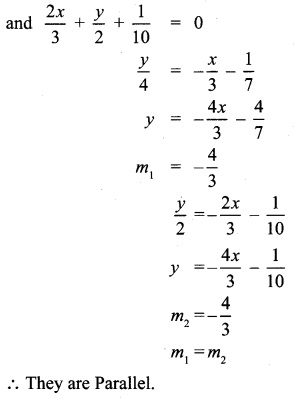
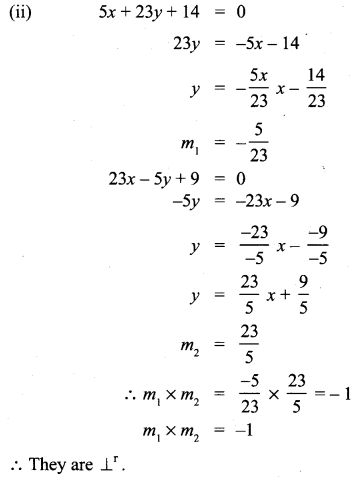
10th Maths Exercise 5.4 Question 4.
If the straight lines 12y = -(p + 3)x + 12, 12x – 7y = 16 are perpendicular then find ‘p’.
Solution:

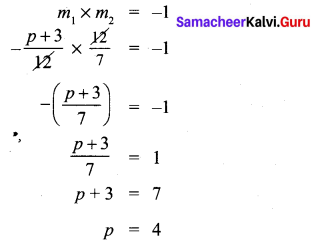
10th Maths Example 5.4 Question 5.
Find the equation of a straight line passing through the point P (-5, 2) and parallel to the line joining the points Q(3, -2) and R(-5, 4).
Solution:
Class 10 Maths Exercise 5.4 Solutions Question 6.
Find the equation of a line passing through ; (6, -2) and perpendicular to the line joining the points (6, 7) and (2, -3).
Solution:
Slope of line joining (6, 7) and (2,-3) is
5 Coordinate Geometry Question 7.
A(-3, 0) B(10, – 2) and C(12, 3) are the vertices of ∆ABC . Find the equation of the altitude through A and B.
Solution:
A(-3, 0), B(10, -2), C(12, 3)
Since AD ⊥ BC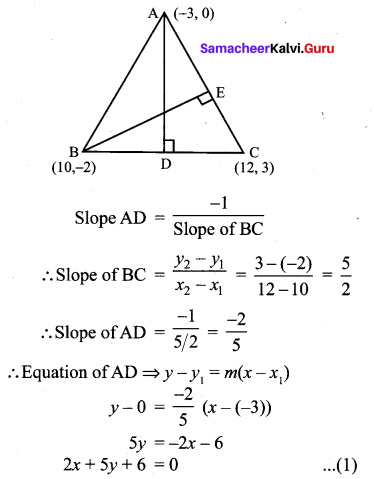
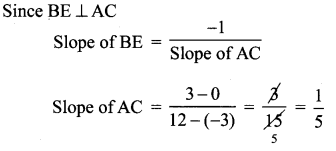
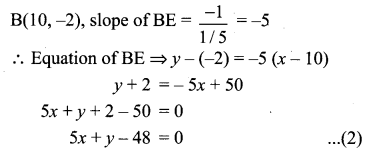
(1), (2) are the required equations of the altitudes through A and B.
5.4 Geometry Question 8.
Find the equation of the perpendicular bisector of the line joining the points A(-4, 2) and B(6, -4).
Solution:
Mid Point AB is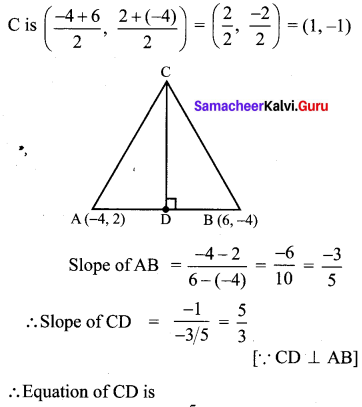
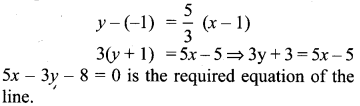
Ex 5.4 Class 10 Question 9.
Find the equation of a straight line through the intersection of lines 7x + 3y = 10, 5x – 4y = 1
and parallel to the line 13x + 5y + 12 = O
Solution: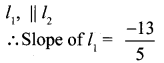
l1 passes through the intersecting point.
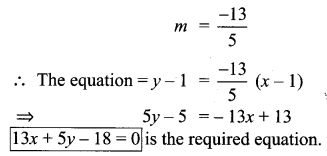
10th Samacheer Kalvi Maths Coordinate Geometry Question 10.
Find the equation of a straight line through the intersection of lines 5x – 6y = 2, 3x + 2y = 10 and perpendicular to the line 4x – 7y + 13 = 0
Solution: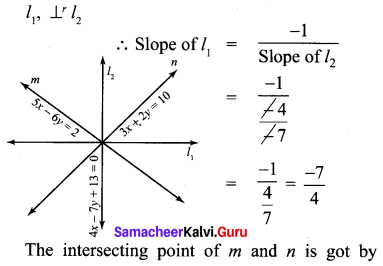


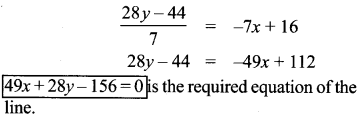
12th Maths Exercise 5.4 Samacheer Kalvi Question 11.
Find the equation of a straight line joining the point of intersection of 3x + y + 2 = 0 and x – 2y – 4 = 0 to the point of intersection of 7x – 3y = -12 and 2y = x + 3
Solution:
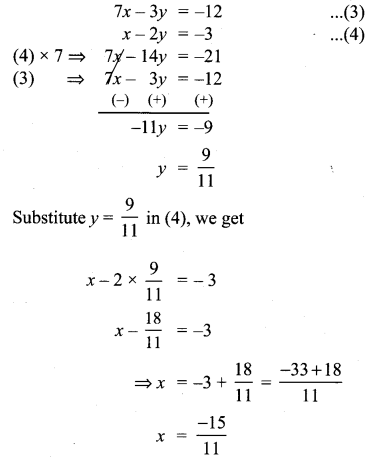

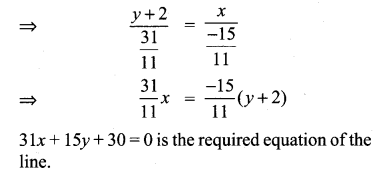
Exercise 5.4 Class 10 Question 12.
Find the equation of a straight line through the point of intersection of the lines 8x + 3+ = 18, 4x + 5+ = 9 and bisecting the line segment joining the points (5, -4) and (-7, 6).
Solution:
The intersecting point of the lines