10th Maths Solutions Chapter 6 Trigonometry Additional Questions

 Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 6 Trigonometry Additional Questions

Question 1.
Given tan A = 43, find the other trigonometric ratios of the angle A.
Solution:
Let us first draw a right ∆ABC.
Now, we know that tan A = BCAB=43
Therefore, if BC = 4k, then AB = 3k, where k is a positive number.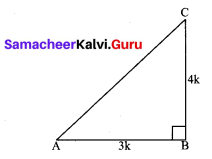

Now, by using the pythagoras theorem, we have
AC2 = AB2 + BC2
= (4k)2 + (3k)2 = 25 k2
AC = 5k
So,
Now, we can write all the trigonometric ratios using their definitions.

Question 2.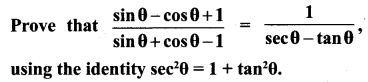

Solution:
Since we will apply the identity involving sec θ and tan θ, let us first convert the LHS (of the identity we need to prove) in terms of sec θ and tan θ by dividing numerator and denominator by cos θ.

Which is the RHS of the identity, we are required to prove.

Question 3.
Prove that sec A (1 – sin A) (sec A + tan A) = 1.
Solution:
LHS = sec A(1 – sin A)(sec A + tan A)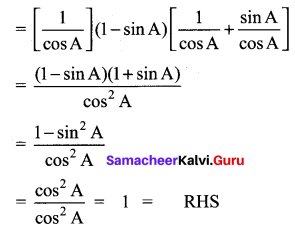

Question 4.
In a right triangle ABC, right-angled at B, if tan A = 1, then verify that 2 sin A cos A = 1.
Solution:
In ABC, tan A = BCAB
Let AB = BC = k, where k is a positive number.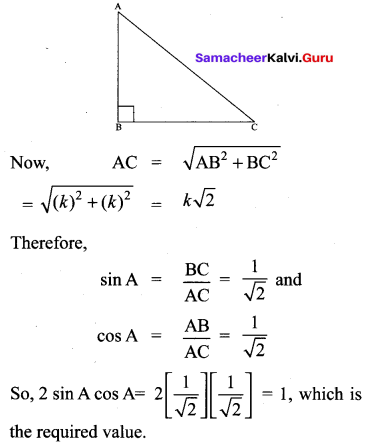

Question 5.
If sin (A – B) = 12, cos (A + B) = 12, 0° < A + B ≤ 90°, A > B, find A and BC
Solution:

We get,
A = 45° and B = 15°

Question 6.
Express the ratios cos A, tan A and sec A in terms of sin A.
Solution:
Since
cos2A + sin2A = 1, therefore,
cos2A = 1 – sin2A
i.e., cos A = ±1−sin2A−−−−−−−−√
This gives cos A = 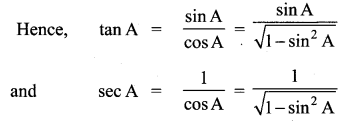1−sin2A

Question 7.
Evaluate tan65∘
Solution:
We know:
cot A = tan(90° – A)
So,

Question 8.
Since sin 3A = cos(A – 26°), where 3A is an acute angle, find the value at A.
Solution:
We are given that sin 3A = cos (A – 26°) ….. (1)
Since sin 3A = cos(90° – 3A) we can write (1) as cos(90° – 3A) = cos(A – 26°)
Since 90° – 3A and A – 26° are both acute angles.
90° – 3A = A – 26°
which gives A = 29°

Question 9.
Express cot 85° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Solution:
cot 85° +cos 75°
= cot(90° – 5°) + cos(90° – 15°)
= tan 5° + sin 15°

Question 10.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides at the river are 30° and 45°, respectively. If the bridge is at a height at 3 m from the banks, find the width at the river.
Solution:
A and B represent points on the bank on opposite sides at the river, so that AB is the width of the river. P is a point on the bridge at a height of 3m i.e., DP = 3 m. We are interested to determine the width at the river which is the length at the side AB of the ∆APB.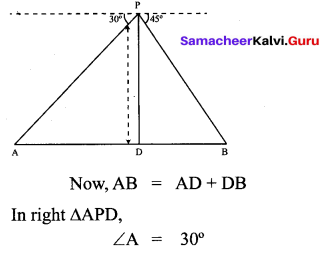


Also, in right ∆PBD,
B = 45°
So, BD = PD = 3 m
Now, AB = BD + AD
= 3 + 33–√ = 3(1 + 3–√)m
Therefore, the width at the river is 3(3–√ + 1)