12maths exercise.2

 Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.2

Question 1.
Find the rank of the following matrices by the minor method: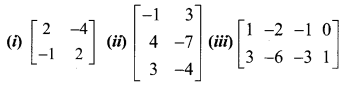


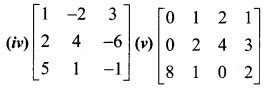
Solution:

Question 2.
Find the rank of the folowing matrices by row reduction method: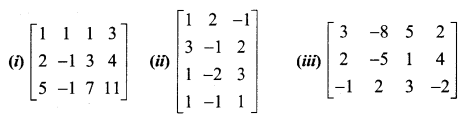

Solution:
(i) Let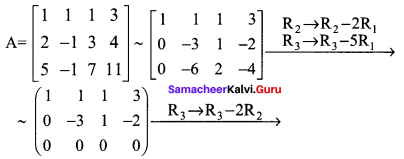

The last equivalent matrix is in row-echelon form. It has three non zero rows. So ρ(A) = 3
(ii) Let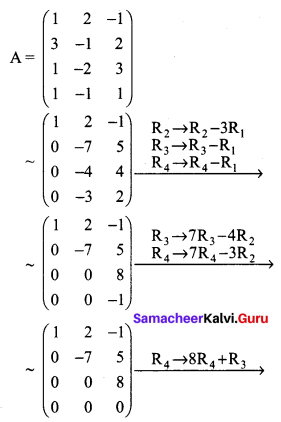

The last equivalent matrix is in row-echelon form. It has three non zero rows. ρ(A) = 3
(iii) Let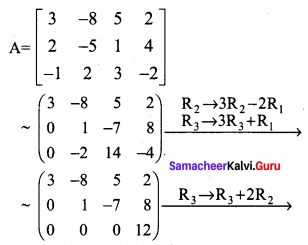

The last equivalent matrix is in row-echelon form. It has three non zero rows. ρ(A) = 3

Question 3.
Find the inverse of each of the following by Gauss-Jordan method: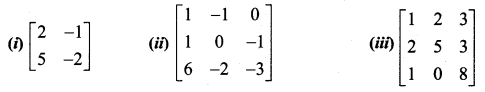

Solution:
(i) Let A=(25−1−2)
Applying Gauss-Jordan method we get

(ii) Let


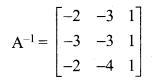
(iii) Let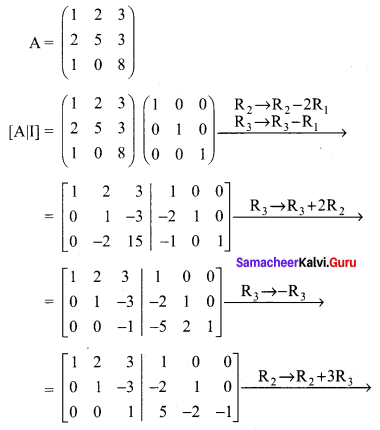

Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.2 Additional Problems

Question 1.
Find the rank of the following matrices.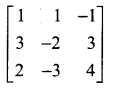 
Solution:

A has at least one non-zero minor of order 2. ρ(A) = 2

Question 2.
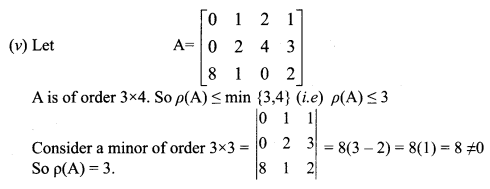
Find the rank of the following matrices.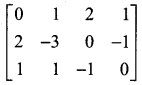 
Solution:

The last equivalent matrix is in the echelon form. It has three non-zero rows.
∴ ρ(A) = 3; Here A is of order 3 × 4

Question 3.
Find the rank of the following matrices.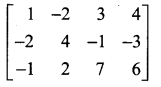 
Solution: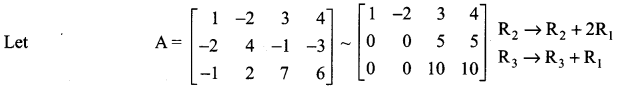


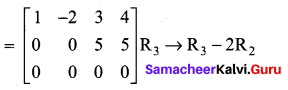
The last equivalent matrix is in the echelon form. The number of non-zero rows in this matrix is two. A is a matrix of order 3 × 4. ∴ ρ(A) = 2

Question 4.
Using elementary transformations find the inverse of the following matrix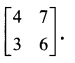 
Solution:

Question 5.
Using elementary transformations find the inverse of the following matrices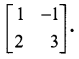 
Solution:

Question 6.
Using elementary transformations find the inverse of the following matrices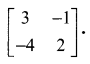 
Solution:

Question 7.
Using elementary transformations, find the inverse of the following matrices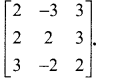 
Solution:

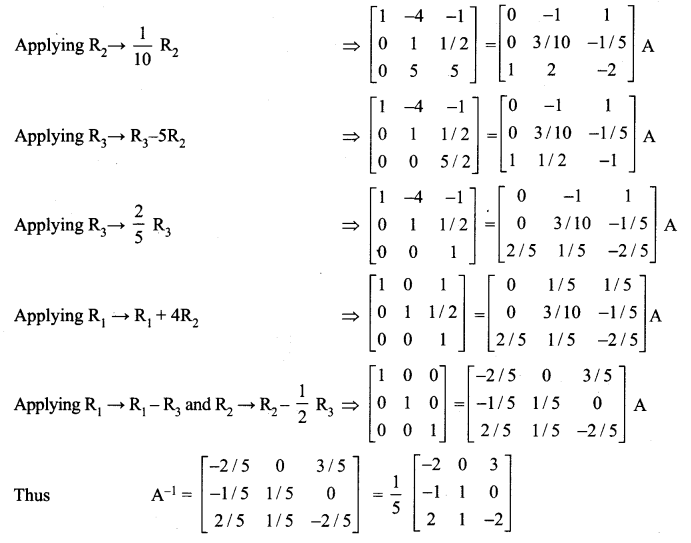
Question 8.
Using elementary transformations, find the inverse of the following matrices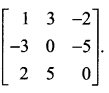 
Solution: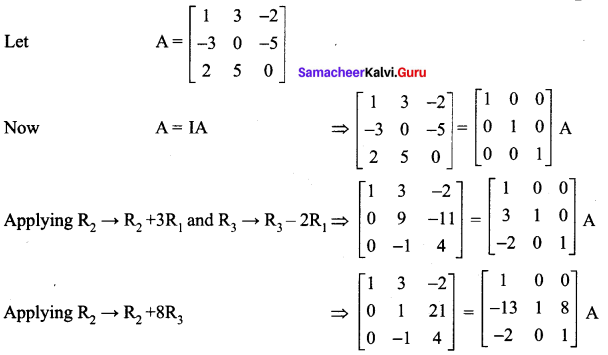

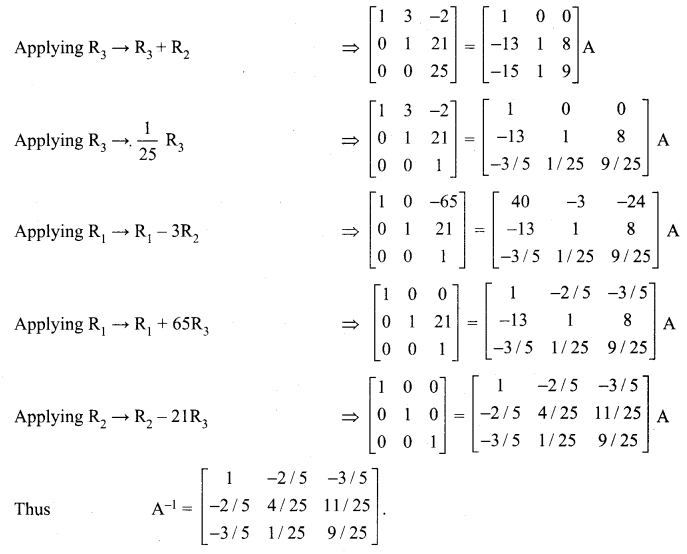
Question 9.
Using elementary transformations, find the inverse of the following matrices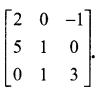 
Solution:

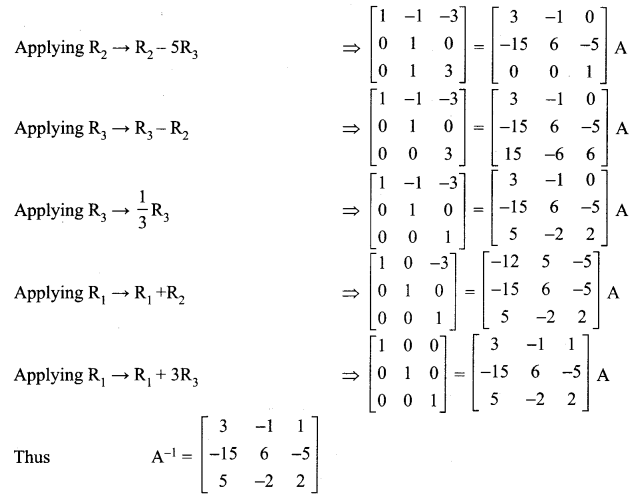
Question 10.
Using elementary transformations, find the inverse of the following matrices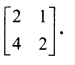 
Solution: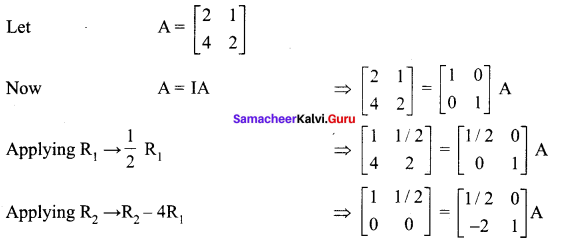

Since R2 has all numbers zero, Thus inverse of matrix A does not exist.